INECUACIONES
En matemática, una inecuación es una desigualdad algebraica en la que aparecen una o más incógnitas en los miembros de la desigualdad.1 2 Si la desigualdad es del tipo  o
o 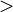 se denomina inecuación en sentido estricto y si es del tipo
se denomina inecuación en sentido estricto y si es del tipo  o
o 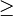 se denomina inecuación en sentido amplio.3
se denomina inecuación en sentido amplio.3
 o
o 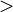 se denomina inecuación en sentido estricto y si es del tipo
se denomina inecuación en sentido estricto y si es del tipo  o
o 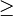 se denomina inecuación en sentido amplio.3
se denomina inecuación en sentido amplio.3
Del mismo modo en que se hace la diferencia de igualdad y ecuación, una inecuación que es válida para todas las variables se llama inecuación incondicional y las que son válidas solo para algunos valores de las variables se conocen como inecuaciones condicionales.4 Los valores que verifican la desigualdad, son sussoluciones.

